metrický prostor

Množina \( P \) zároveň s funkcí \( \rho(x, y) \) dvou proměnných \( x \in P \), \( y \in P \), která má tyto vlastnosti:
\( \rho(x, y) = 0 \) právě když \( x = y \);
\( \rho(x, y) = \rho(y, x) \);
\( \rho(x, z) \leq \rho(x, y) + \rho(y, z) \) (trojúhelníková nerovnost).
Metrický prostor se značí zpravidla \( (P, \rho) \).
Funkce \( \rho(x, y) \) se nazývá metrika a číslo \( \rho(x, y) \) vzdálenost bodu \( x \) od bodu \( y \).

Příklady metrických prostorů:

a) číselná osa s metrikou \( \rho(x, y) = |x - y| \);
b) rovina s metrikou \( \rho(X, Y) = |X - Y| \) (velikost úsečky \( XY \));
c) množina spojitých funkcí \( f \) na intervalu \( \langle 0, 1 \rangle \) s metrikou \( \rho(f_1, f_2) = \max |f_1(t) - f_2(t)| \), \( t \in \langle 0, 1 \rangle \).

Okolí bodu v metrickém prostoru je množina všech bodů \( x \), jejichž vzdálenost od \( a \) je menší než \( r \) (kladné číslo, tzv. poloměr okolí).
Metrický prostor je tedy topologickým prostorem.
V metrickém prostoru se definuje:
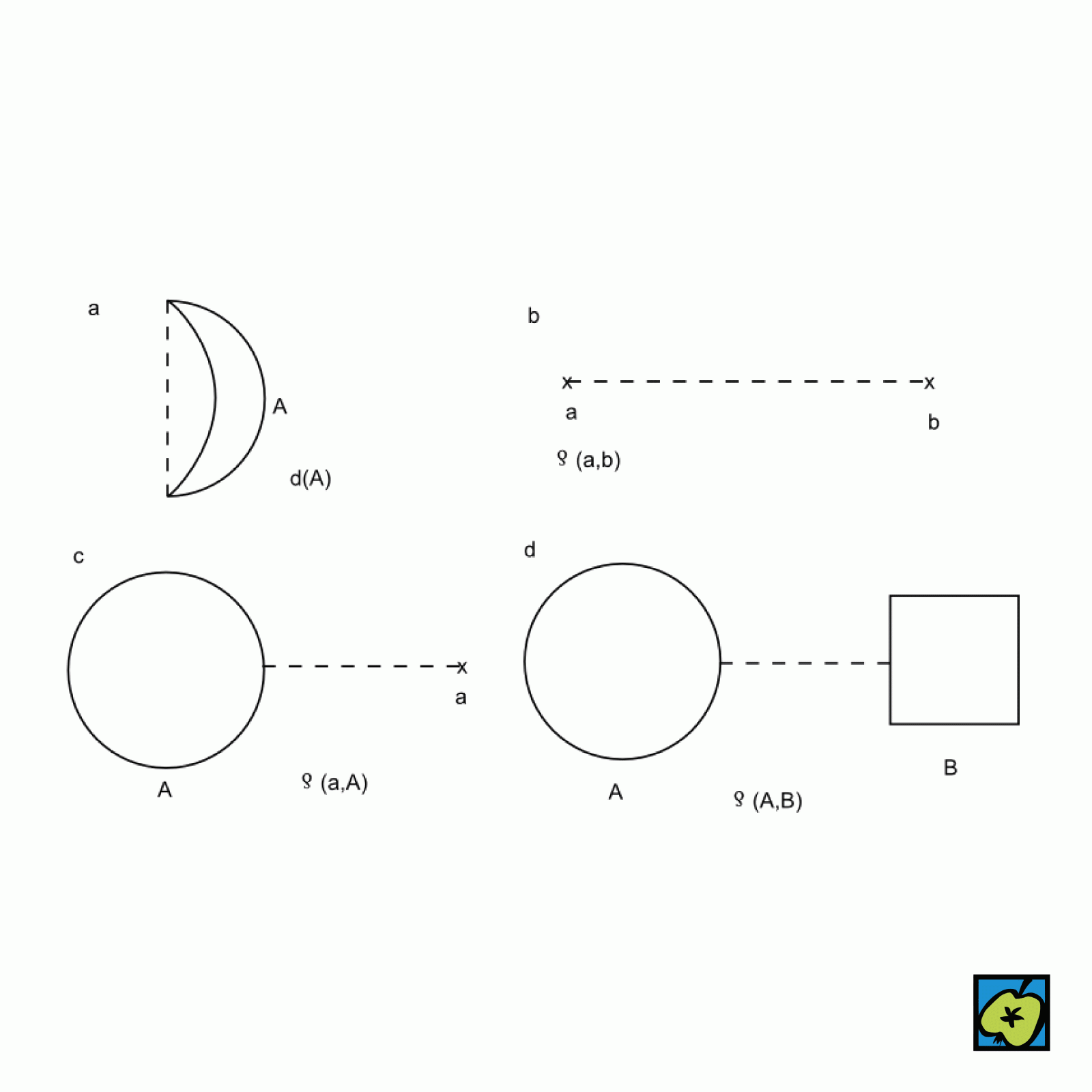
vzdálenost \( \rho(a, A) = \inf \rho(a, x), \; x \in A \) bodu \( a \) od množiny \( A \);
vzdálenost \( \rho(A, B) = \inf \rho(x, y), \; x \in A, \; y \in B \) dvou množin \( A \) a \( B \);
průměr \( d(A) = \sup \rho(x, y), \; x \in A, \; y \in A \) množiny \( A \).