úhel

Geometrie

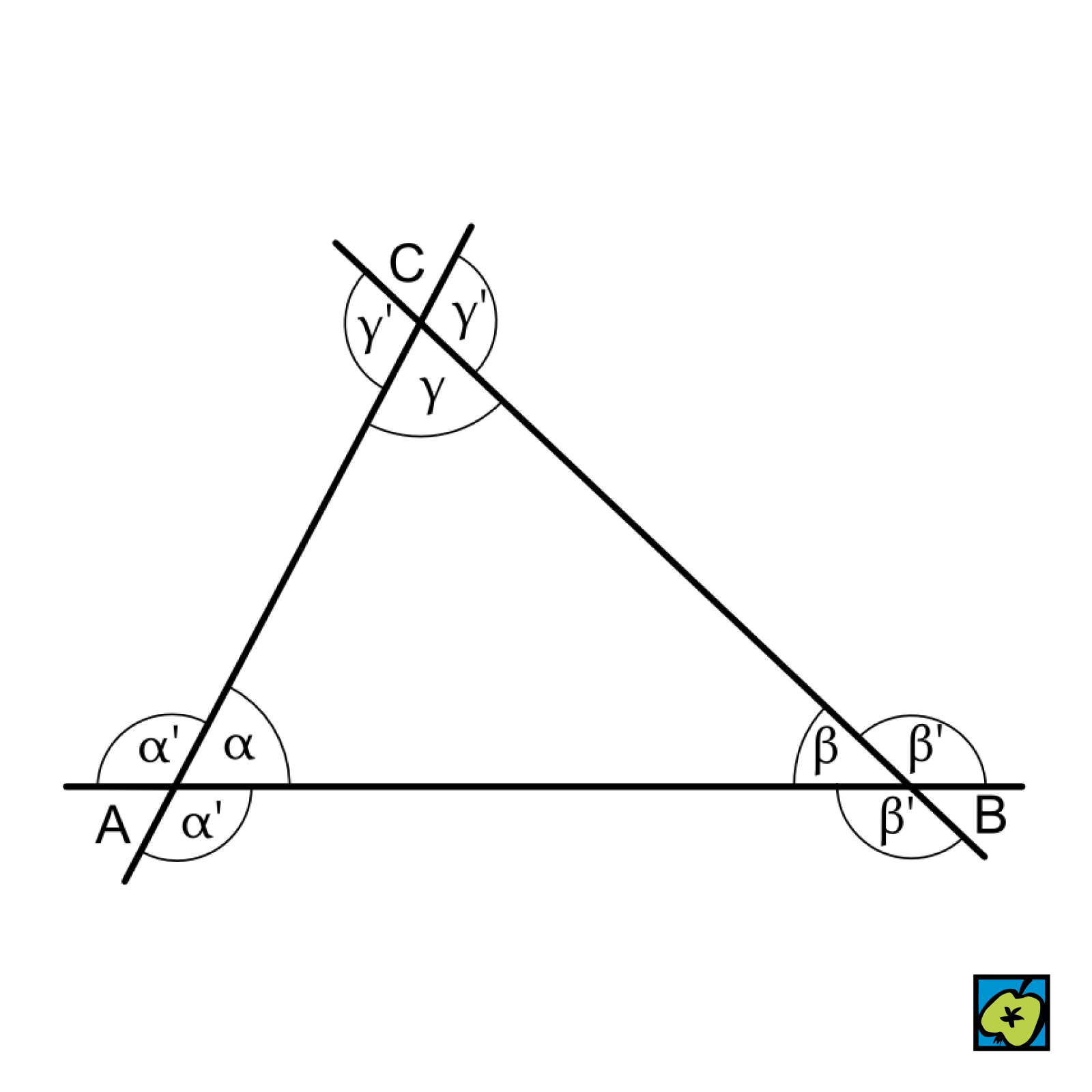
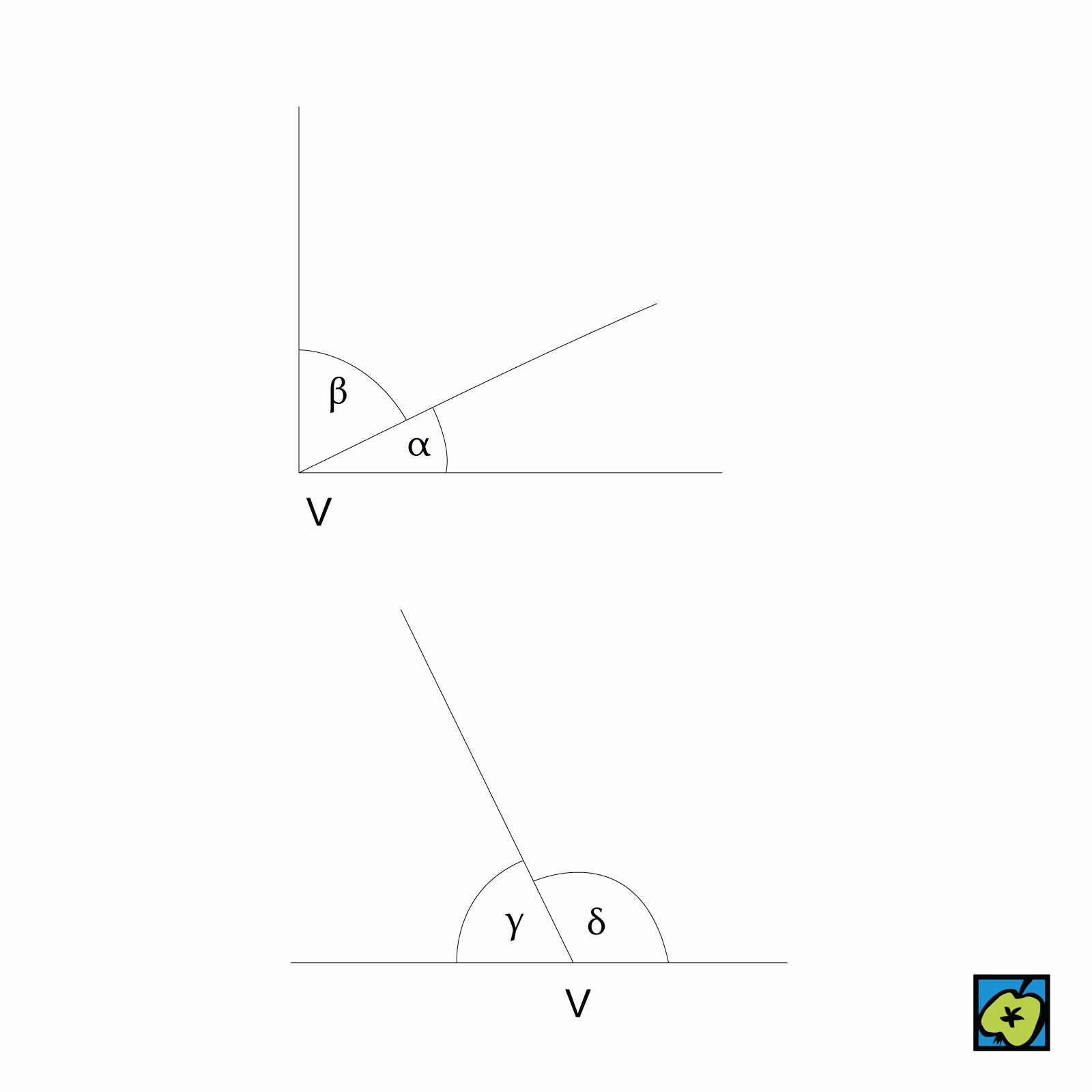
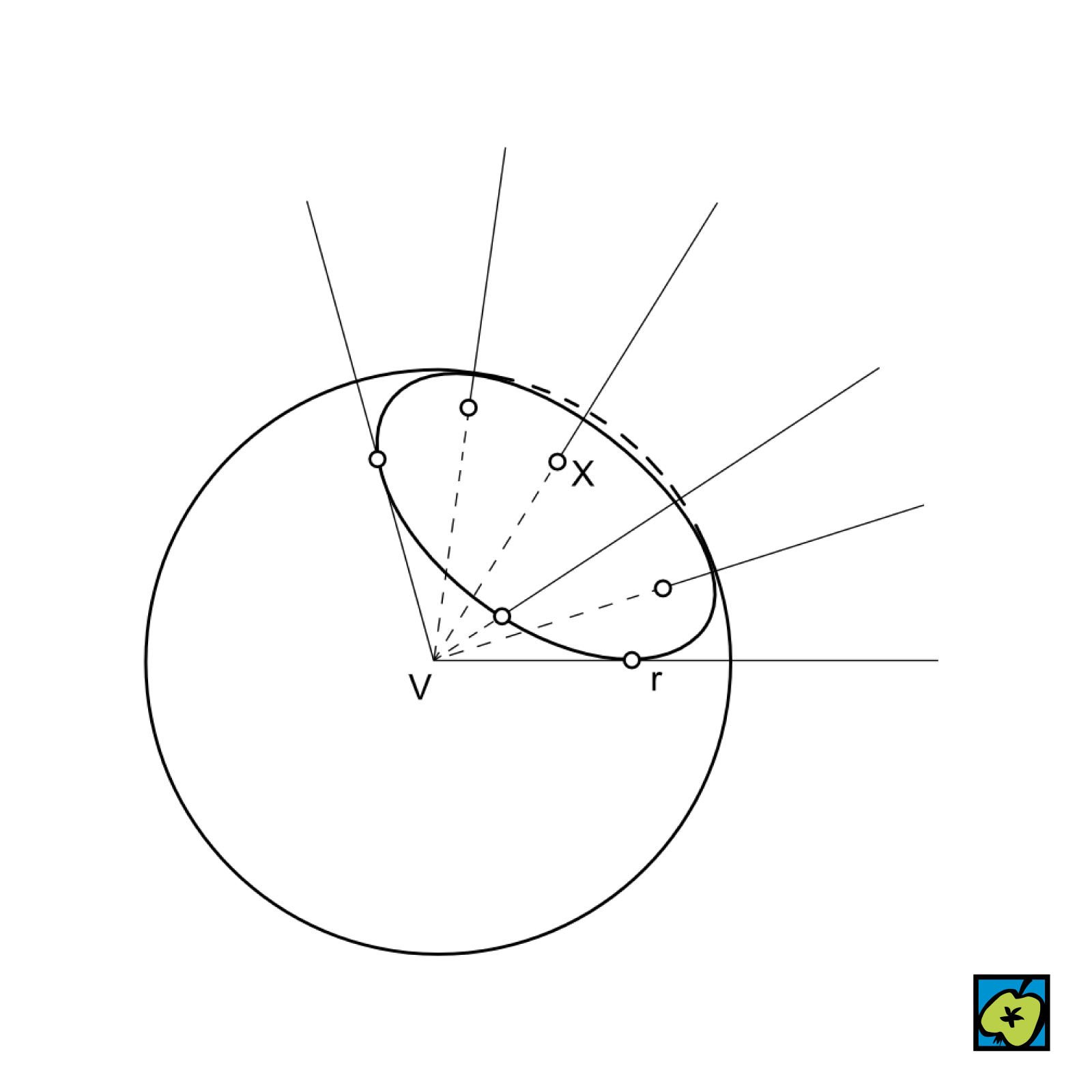
Základní geometrický útvar, nejčastěji rovinný úhel, definovaný takto: Je-li dán oblouk AB na kružnici se středem V a poloměrem r= 1, rovinným úhlem se rozumí množina všech bodů všech polopřímek o počátku V, které protínají oblouk AB. Bod V je vrchol úhlu, polopřímky VA, VB ramena úhlu. Je-li oblouk AB polokružnice, získá se přímý úhel AVB, je-li oblouk AB podmnožinou nějaké polokružnice, jde o konvexní úhel. Je-li některá polokružnice vlastní podmnožinou oblouku AB, získá se nekonvexní úhel. Mezní případy: nulový úhel (při nulové délce oblouku AB) a plný úhel (je-li AB celá kružnice). Velikost rovinného úhlu AVB se odvodí z délky oblouku AB na jednotkové kružnici a vyjádří se v radiánech nebo ve stupních. Úhel AVB má velikost 1 radián (1 rad), je-li oblouk AB dlouhý 1 m a je částí kružnice s poloměrem 1 m. Úhel AVB má velikost 1 stupeň (1°), je-li oblouk AB dlouhý pí/180 m a je částí kružnice s poloměrem 1 m (1 rad= 58° 17' 45“). Zapisuje-li se velikost úhlu v radiánech (resp. ve stupních), mluví se o obloukové (resp. stupňové) míře úhlu. Další jednotky ve stupňové míře: 1 minuta (1') pro 1 /60 stupně, 1 vteřina (1“) pro 1/60 minuty. Úhel, jehož velikost je 90°, je pravý, 180° přímý, 360° plný. Je-li velikost úhlu mezi 0° a 90° (resp. mezi 90° a 180°), je úhel ostrý (resp. tupý). Ve stejných jednotkách jako rovinný úhel se měří velikost úhlu otočení (může být větší než 360°). Orientovaný úhel je uspořádaná dvojice polopřímek se společným počátkem (vyznačuje se šipkou na oblouku kružnice). Prostorový úhel se definuje obdobně jako úhel rovinný, ale oblouk kružnice se nahradí kulovým vrchlíkem. Velikost prostorového úhlu se měří ve steradiánech.

Vytvořeno: 14. 3. 2000
Aktualizováno: 13. 3. 2003
Autor: -red-

Odkazující hesla: minuta, paralaktický úhel, Russellovy úhly, směrník, úhlová vzdálenost.