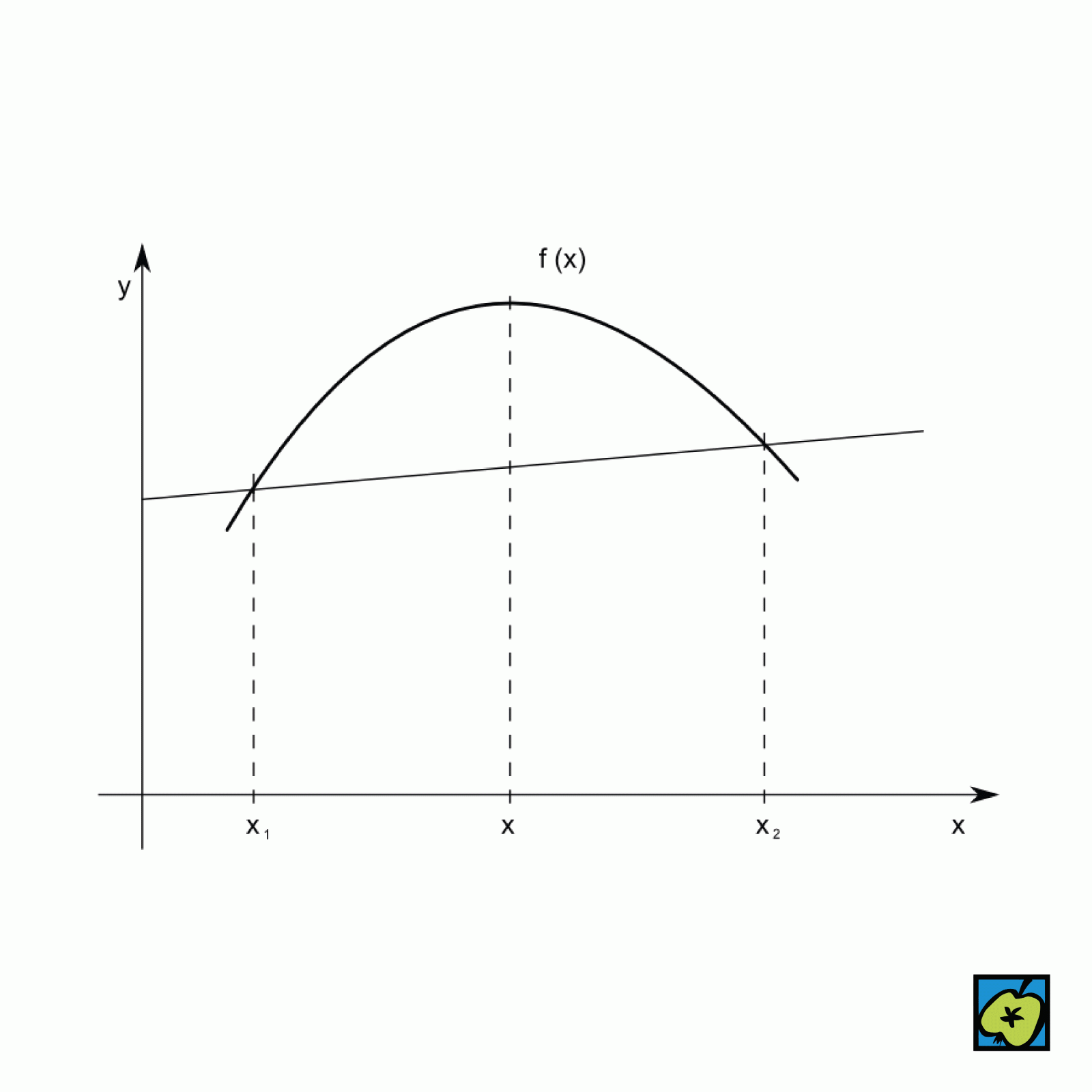konkávní

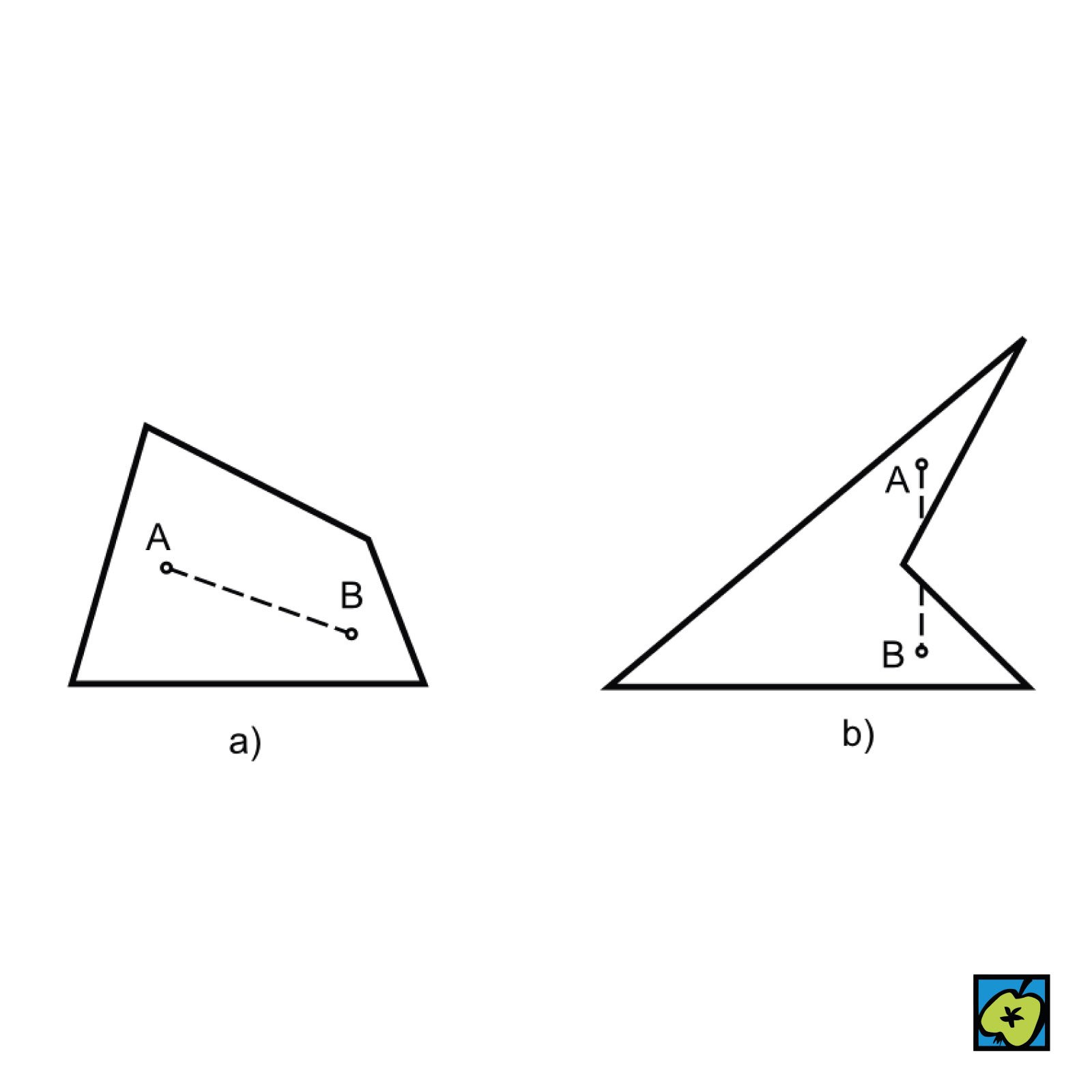
Vlastnost matematických funkcí, geometrických objektů (křivek, ploch) nebo množin, která označuje tvar prohnutý směrem dovnitř (opakem je konvexní). Reálná funkce \( f \) jedné proměnné je konkávní na intervalu \( J \), pokud pro libovolné body \( x_1 \), \( x_2 \) z \( J \) a každé číslo \( t \) (\(0 \leq t \leq 1\)) platí nerovnost:

\[ f(tx_1 + (1 - t)x_2) \geq t f(x_1) + (1 - t) f(x_2) \]

Geometricky to znamená, že graf funkce v každém bodě intervalu leží nad nebo právě na úsečce spojující libovolné dva body grafu v tomto intervalu. Konkávnost lze také určit pomocí druhé derivace funkce: pokud

\[ \frac{d^2 f}{dx^2} \leq 0, \]

je funkce konkávní na daném intervalu. Příkladem konkávní funkce je \( \sin x \) na každém intervalu typu \((2n\pi, (2n+1)\pi)\), kde \( n = 0, \pm1, \pm2, \dots \) Dalším příkladem je logaritmická funkce, která je konkávní na celém definičním oboru.