fyzické kyvadlo

Fyzika

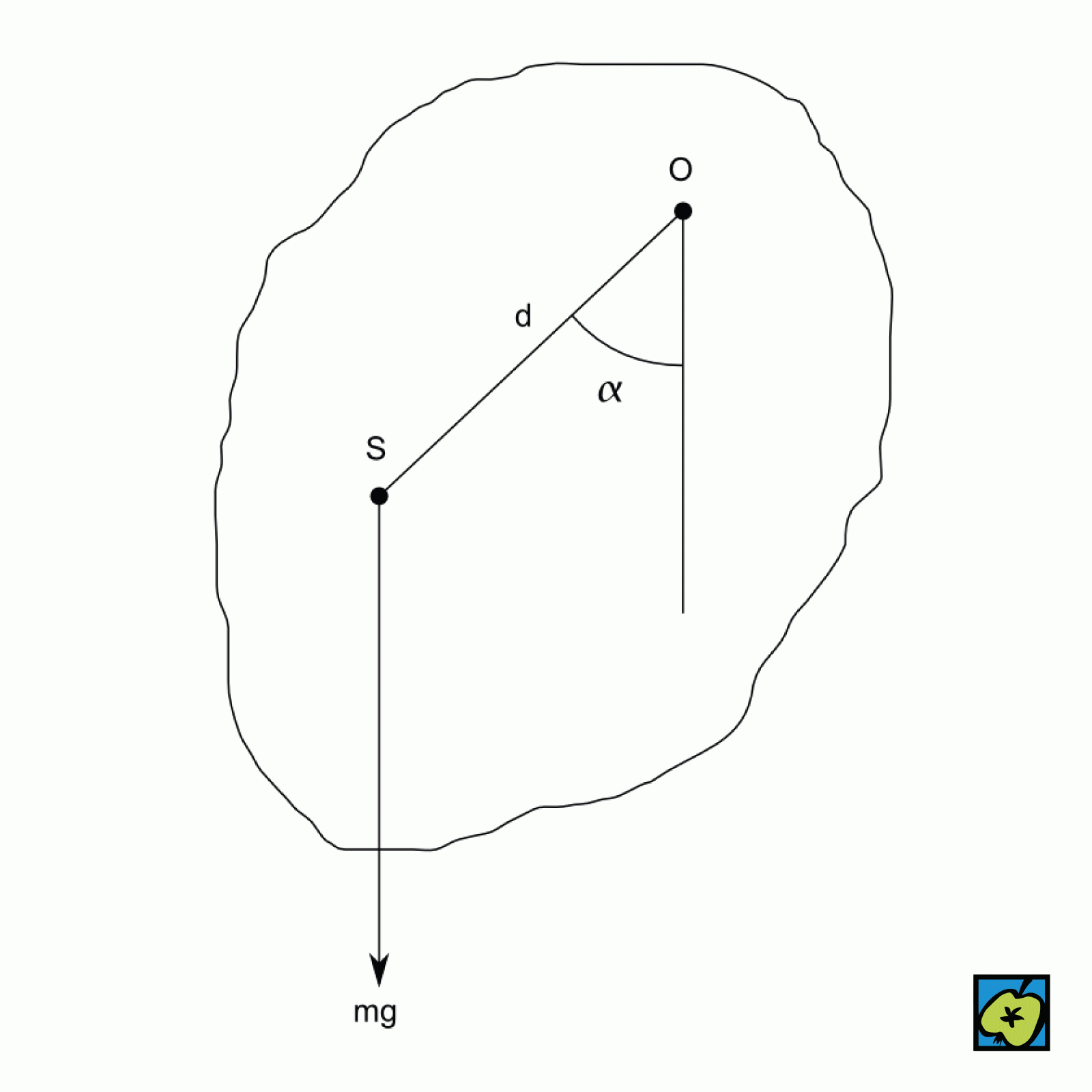
Těleso volně otočné kolem vodorovné osy o, která neprochází jeho těžištěm S; po vychýlení z rovnovážné polohy se v tíhovém poli kýve. Pro malé výchylky je pohyb harmonický a doba kmitu

\( T \;=\; 2\pi \sqrt{\frac{J}{m g d}} \)

kde m je hmotnost kyvadla, g tíhové zrychlení, d vzdálenost těžiště S od osy otáčení o a J moment setrvačnosti vůči ose o. Pro výpočet J platí Steinerova věta \( J = J_S + m d^2 \), kde \( J_S \) je moment setrvačnosti vůči rovnoběžné ose procházející těžištěm.

Často se zavádí tzv. redukovaná délka \( L_r = \dfrac{J}{m d} \),

takže \( T = 2\pi \sqrt{\dfrac{L_r}{g}} \).

Pro malé úhly (např. \( |\varphi| \lesssim 10^\circ \)) je kyv téměř izochronní; obecně však perioda s amplitudou mírně roste.

Vytvořeno: 14. 3. 2000
Aktualizováno: 15. 8. 2025
Autor: -red-

Odkazující hesla: horizontální kyvadlo, krok hodin, náklonoměr, tíhové pole Země.

Vyzkoušejte si s přáteli Kvízy encyklopedie CoJeCo.cz!