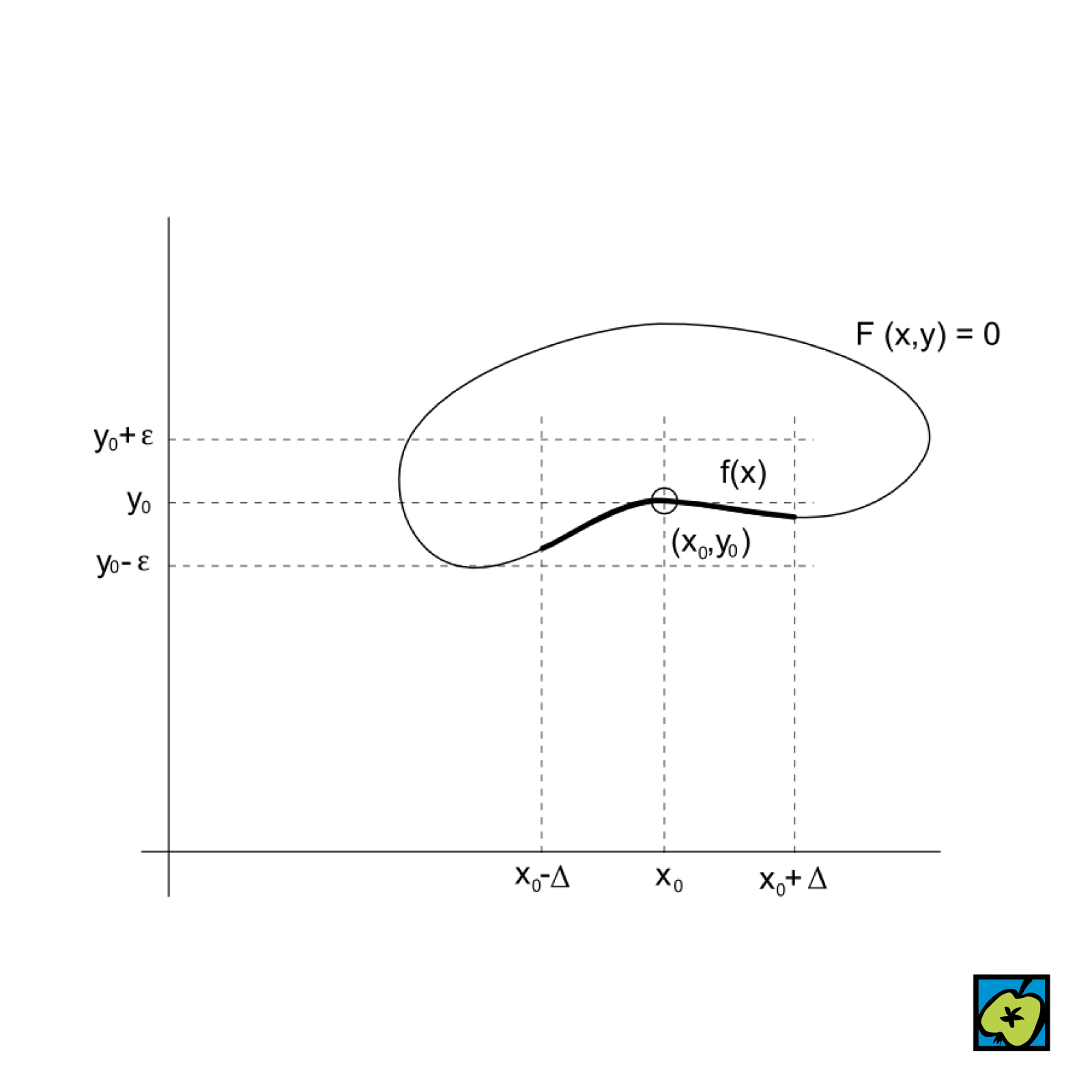
věta o implicitní funkci

Jedna ze základních vět o řešení rovnic tvaru \( F(x, y) = 0 \). Pokud existuje funkce \( f(x) \) taková, že \( F(x, f(x)) = 0 \), pak se funkce \( f \) nazývá implicitně určenou funkcí. Nejjednodušší varianta věty říká: nechť \( X \) a \( Y \) jsou podmnožiny reálných čísel a bod \( (x_0, y_0) \) je vnitřním bodem kartézského součinu \( X \times Y \). Je-li funkce \( F : X \times Y \rightarrow \mathbb{R} \) spojitá v okolí bodu \( (x_0, y_0) \), platí-li \( F(x_0, y_0) = 0 \) a existují-li kladná čísla \( \delta > 0 \) a \( \varepsilon > 0 \) tak, že pro každé pevné \( x \in (x_0 - \delta, x_0 + \delta) \) je funkce \( F(x, y) \) přísně monotónní v proměnné \( y \) na intervalu \( (y_0 - \varepsilon, y_0 + \varepsilon) \), pak existuje jediná spojitá funkce \( f : (x_0 - \Delta, x_0 + \Delta) \rightarrow (y_0 - \varepsilon, y_0 + \varepsilon) \), kde \( \Delta > 0 \), taková, že \( F(x, f(x)) = 0 \) pro všechna \( x \in (x_0 - \Delta, x_0 + \Delta) \) a \( f(x_0) = y_0 \). Jsou-li navíc splněny předpoklady o parciálních derivacích funkce \( F \), má funkce \( f \) derivace, které lze spočítat. Složitější varianty těchto tvrzení jsou obsahem obecnějších vět o implicitní funkci.