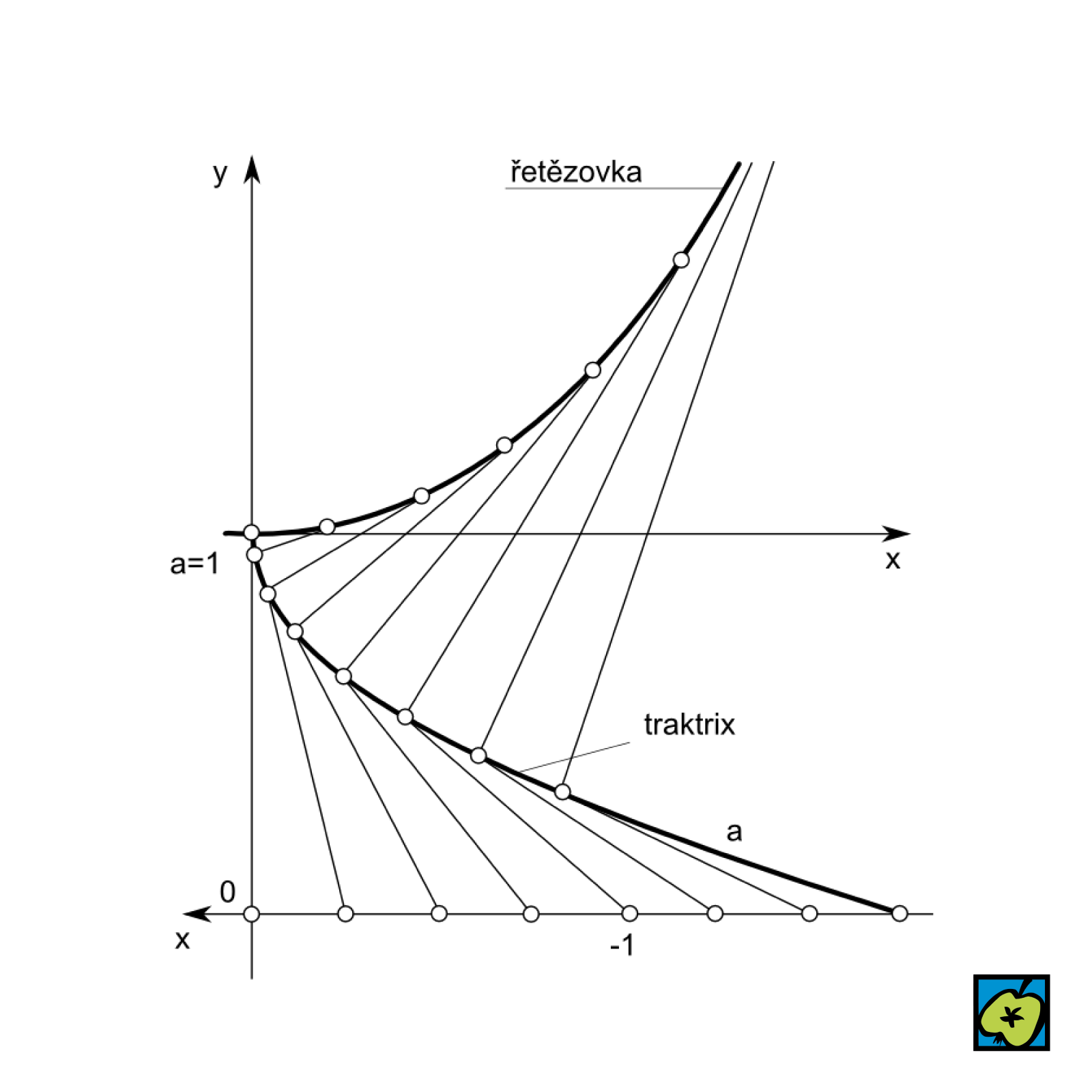
traktrix

[Latina], evolventa řetězovky, rovinná křivka, která má kartézskou rovnici (standardní poloha, asymptota \(y=0\), bod \((0,a)\)):

\[ x \;=\; a\,\ln\!\left(\frac{a+\sqrt{a^{2}-y^{2}}}{\,y\,}\right)\; -\; \sqrt{a^{2}-y^{2}}, \qquad 0< y \le a\],

Pro každou tečnu je vzdálenost bodu dotyku a průsečíku s osou x konstantní (je rovna číslu a). Model: tažený bod po rovině za provázek délky \(a\), jehož druhý konec klouže po ose x). Po otočení kolem asymptoty vytváří pseudokouli (tractricoid) s konstantní Gaussovou křivostí \(K=-1/a^{2}\).

Diferenciální rovnice (z definice konstantní délky tečny):

\[ \frac{\mathrm{d}y}{\mathrm{d}x} \;=\; -\,\frac{\sqrt{a^{2}-y^{2}}}{\,y\,}, \qquad y\in(0,a]. \]

Parametrické vyjádření (hyperbolický parametr \(t\ge 0\)):

\[ x(t) = a\,\big(t-\tanh t\big), \qquad y(t) = a\,\operatorname{sech} t. \]

Průsečík s osou y v bodě \((0,a)\), asymptota \(y=0\) pro \(x\to +\infty\); délka tečného úseku k ose x v libovolném bodě rovna \(a\). Etymologie názvu vychází z latinského trahere – „táhnout“.