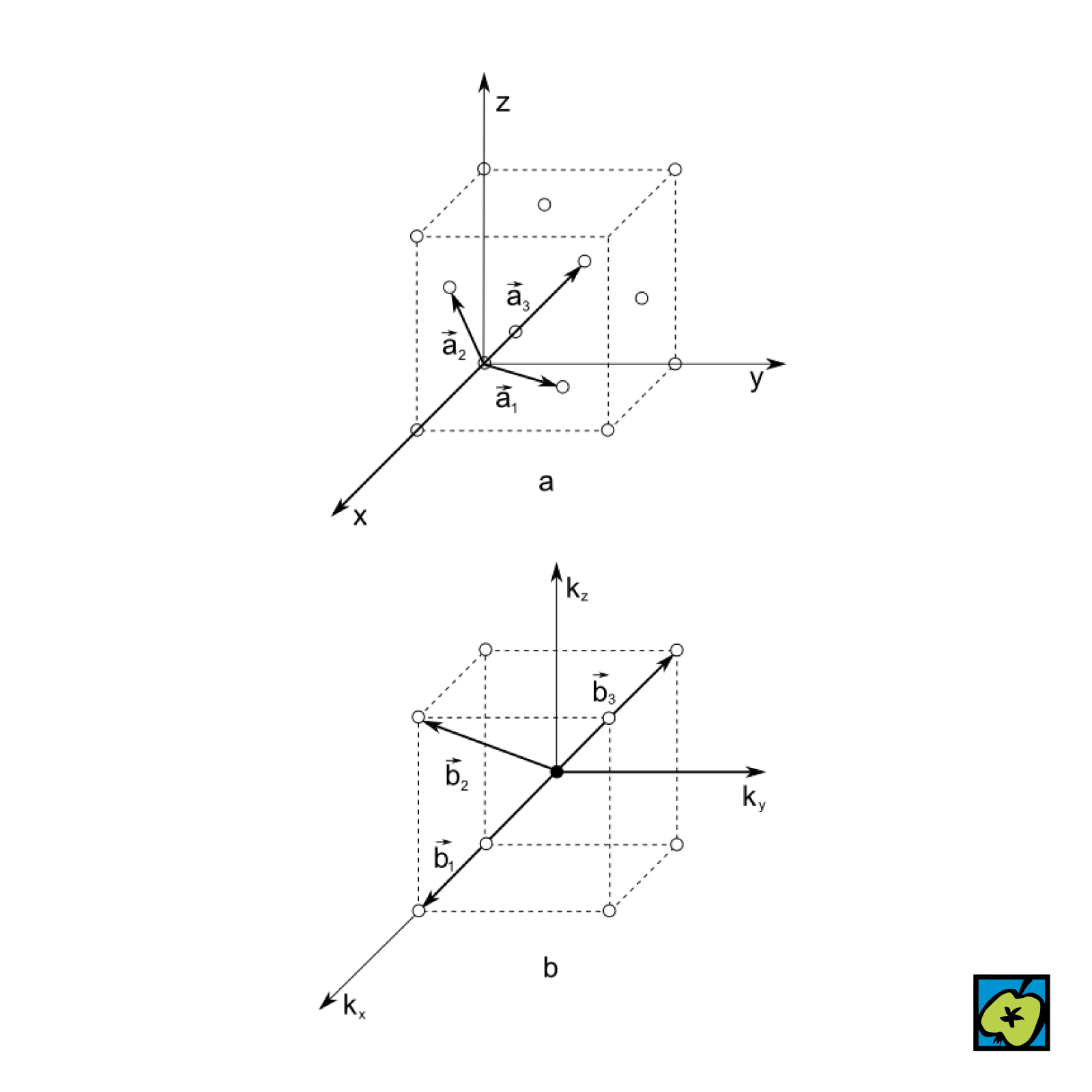
reciproká mřížka

Prostorová mřížka, jejíž body jsou určeny polohovými vektory r = n₁b₁ + n₂b₂ + n₃b₃, kde n₁, n₂, n₃ jsou celá čísla a vektory b₁, b₂, b₃ se nazývají primitivní translanční vektory reciproké mřížky. Jsou plně určeny trojicí vektorů a₁, a₂, a₃ – primitivními vektory translační přímé mřížky, tj. mřížky dané krystalové struktury, k níž reciproká mřížka náleží. Platí: b₁ = 2π a₂ x a₃ / a₁.a₂.a₃ (atd. cyklickou záměnou a_i.b_i = 2πδ_ij, kde δ_ij = 1 pro i = j δ_ij = 0 pro i≠j). Například k plošně centrované kubické mřížce je reciproká mřížka kubická prostorově centrovaná mřížka. Má význam v kvantové teorii pevných látek při popisu stavu elektronů.