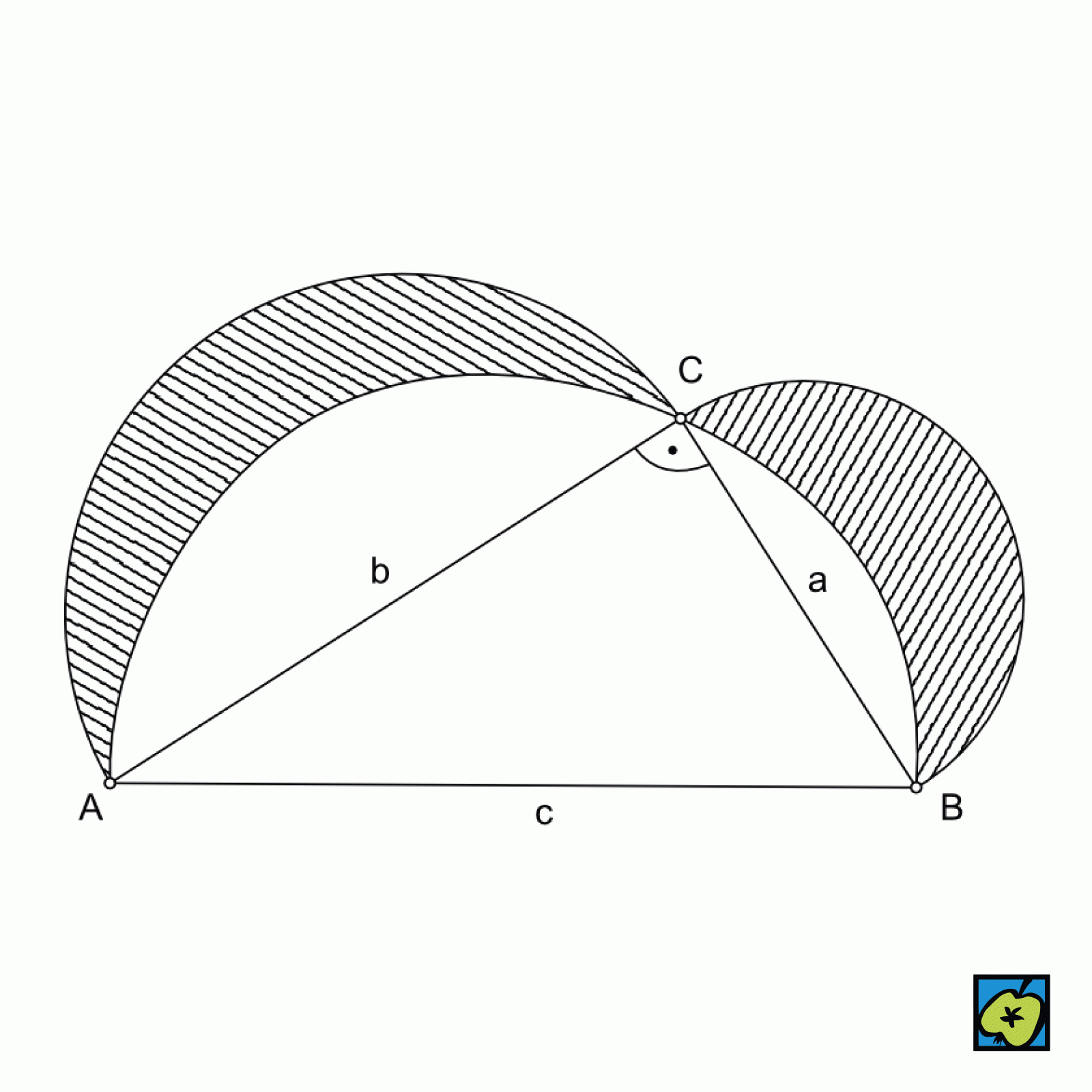
Hippokratovy půlměsíčky

Geometrie

Dva útvary v podobě půlměsíčků vytvořené v rovině nad odvěsnami pravoúhlého trojúhelníku. Hranici každého Hippokratova půlměsíčku tvoří jednak půlkružnice sestrojená nad příslušnou odvěsnou jako nad průměrem, jednak oblouk kružnice sestrojené nad přeponou jako nad průměrem. Součet obsahů obou Hippokratových půlměsíčků se rovná obsahu tohoto trojúhelníka. Z historického hlediska měly Hippokratovy půlměsíčky význam v souvislosti s úlohou o kvadratuře kruhu.

Vytvořeno: 14. 3. 2000
Aktualizováno: 15. 8. 2025
Autor: -red-

Vyzkoušejte si s přáteli Kvízy encyklopedie CoJeCo.cz!