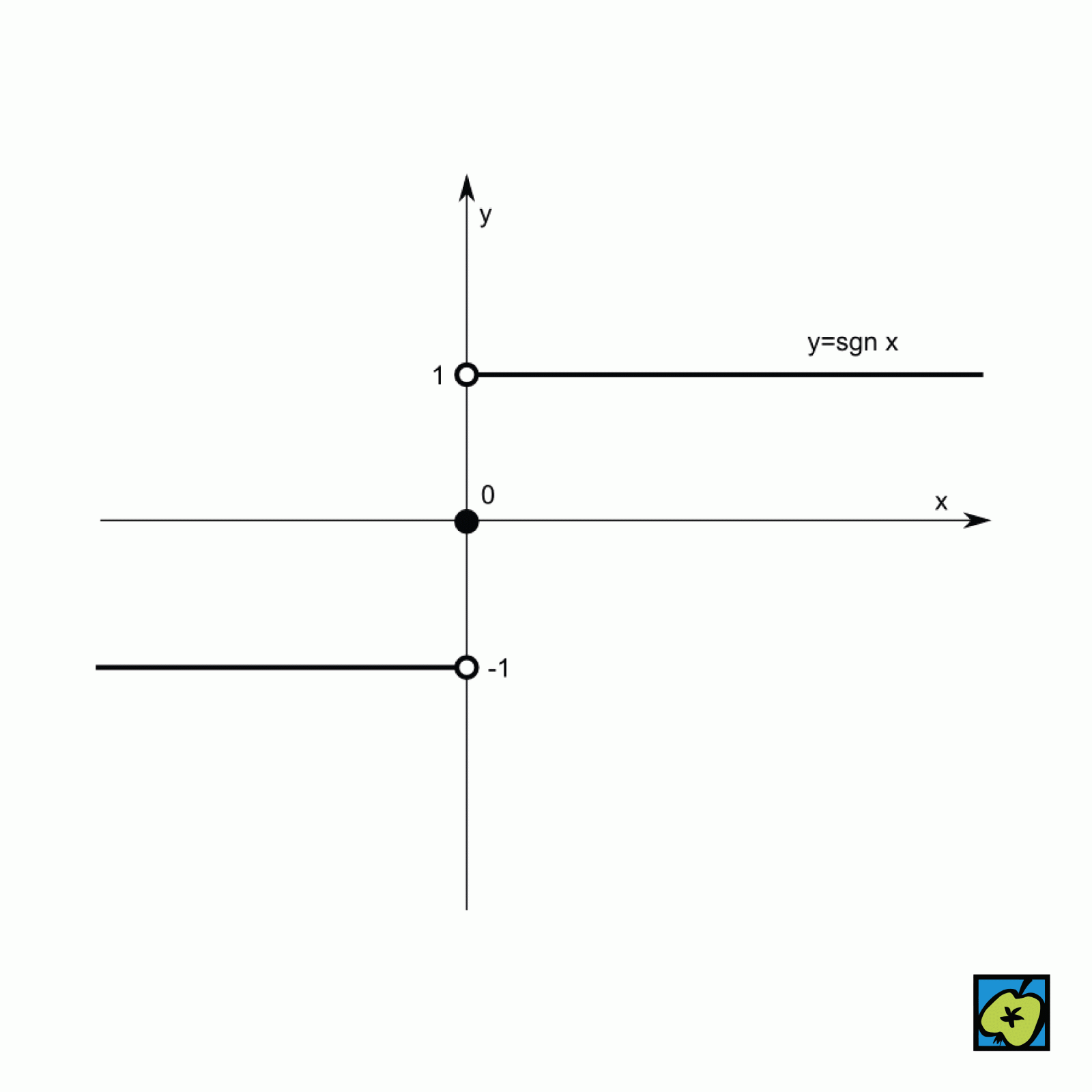funkce signum

Též znaménková funkce, značená sgn (x), případně sign (x), funkce reálné proměnné s definičním oborem \(\mathbb{R}\) a oborem hodnot \(\{-1,0,1\}\), která vrací „znaménko“ čísla (sgn z latinského signum): \( \operatorname{sgn}(x)=\begin{cases}-1,& x<0\\[2pt] 0,& x=0\\[2pt] 1,& x>0\end{cases} \).

Pro každé \(x\) platí \(x\cdot \operatorname{sgn}(x)=|x|\) a pro \(x\neq 0\) také \( \operatorname{sgn}(x)=\dfrac{x}{|x|} \).

Základní vlastnosti: lichost \( \operatorname{sgn}(-x)=-\operatorname{sgn}(x)\), násobivost \(\operatorname{sgn}(xy)=\operatorname{sgn}(x)\operatorname{sgn}(y)\), pro \(a\neq 0\) \(\operatorname{sgn}(ax)=\operatorname{sgn}(a)\operatorname{sgn}(x)\). Funkce je nespojitá v bodě \(x=0\) (skok o 2), na intervalech \((-\infty,0)\) a \((0,\infty)\) konstantní; pro \(x\neq 0\) navíc \(\operatorname{sgn}(|x|)=1\).

Vztahy k dalším funkcím: \( \dfrac{\mathrm{d}}{\mathrm{d}x}|x|=\operatorname{sgn}(x)\) pro \(x\neq 0\) a tedy \(\int \operatorname{sgn}(x)\,\mathrm{d}x=|x|+C\). Ve smyslu zobecněných funkcí \( \dfrac{\mathrm{d}}{\mathrm{d}x}\operatorname{sgn}(x)=2\,\delta(x)\). Vztah ke skokové (Heavisideově) funkci: pro \(x\neq 0\) \( \operatorname{sgn}(x)=2H(x)-1=H(x)-H(-x)\) (hodnota v nule dle zvolené konvence).