exponenciála

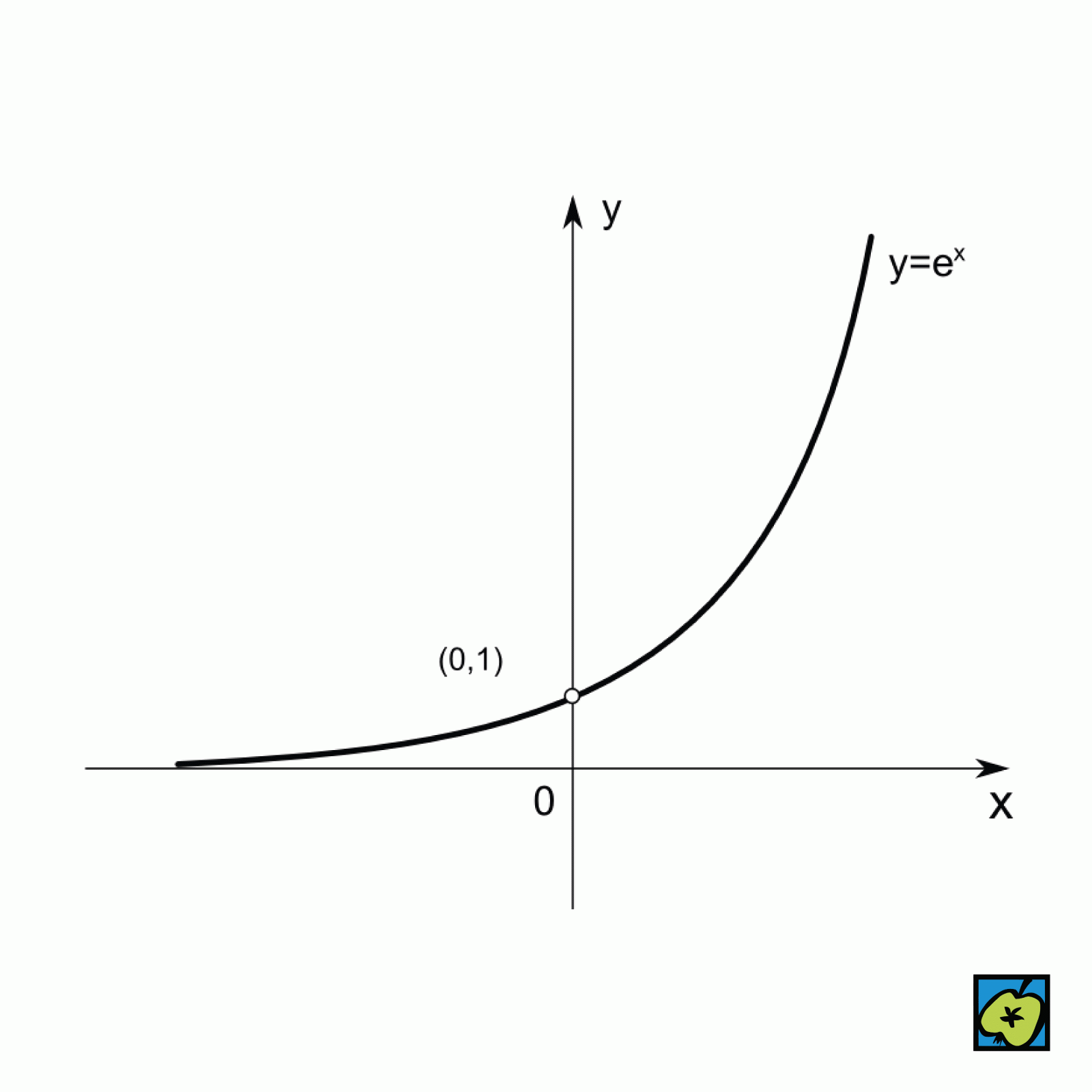
[Latina], grafické znázornění exponenciální funkce, často se tímto pojmem označuje i samotná funkce tvaru \( f(x) = a^x \), kde \( a > 0 \) a \( a \neq 1 \). Zvláštní význam má přirozená exponenciální funkce \( e^x \), kde základ \( e \approx 2{,}71828 \) je Eulerovo číslo. Graf exponenciální funkce se vyznačuje rychlým růstem pro kladné hodnoty argumentu (pokud \( a > 1 \)) a exponenciálním poklesem pro záporné hodnoty. Exponenciála se používá k popisu mnoha přírodních a technických jevů, například radioaktivního rozpadu, růstu populace, úročení kapitálu či tlumených kmitů. V matematické analýze je exponenciála definována také pomocí nekonečné mocninné řady \(\sum_{n=0}^{\infty} \frac{x^n}{n!}\). Má jedinečné vlastnosti, například derivace i integrál funkce \( e^x \) jsou totožné s původní funkcí. V komplexní analýze souvisí exponenciála s trigonometrickými funkcemi prostřednictvím Eulerova vzorce  \( e^{ix} = \cos x + i \sin x \). Pojem exponenciála se používá i v lineární algebře při definici maticové exponenciály, důležité například v řešení soustav diferenciálních rovnic.