dikritický uzel
Matematika
[Dykritycký], bod rovnováhy autonomního lineárního systému ve tvaru \( x_i = a_{i1}x_1 + a_{i2}x_2 \), \( i = 1,2 \), který má charakteristickou rovnici s jediným vlastním číslem \( \lambda \). Pokud je \( \lambda \) < 0, jde o stabilní dikritický uzel, při \( \lambda \) > 0 o nestabilní. V obou případech mají řešení tvar přímek sbíhajících se nebo rozbíhajících z rovnovážného bodu, bez spirálovitého chování. Systém lze převést do Jordanovy normální formy. Geometricky se jedná o zvláštní typ uzlového bodu s jediným vlastním směrem. V teorii dynamických systémů představuje hraniční případ mezi uzlem a ohniskem.
Vytvořeno:
14. 3. 2000
Aktualizováno:
6. 8. 2025
Autor: -red-
Vyzkoušejte si s přáteli Kvízy encyklopedie CoJeCo.cz!
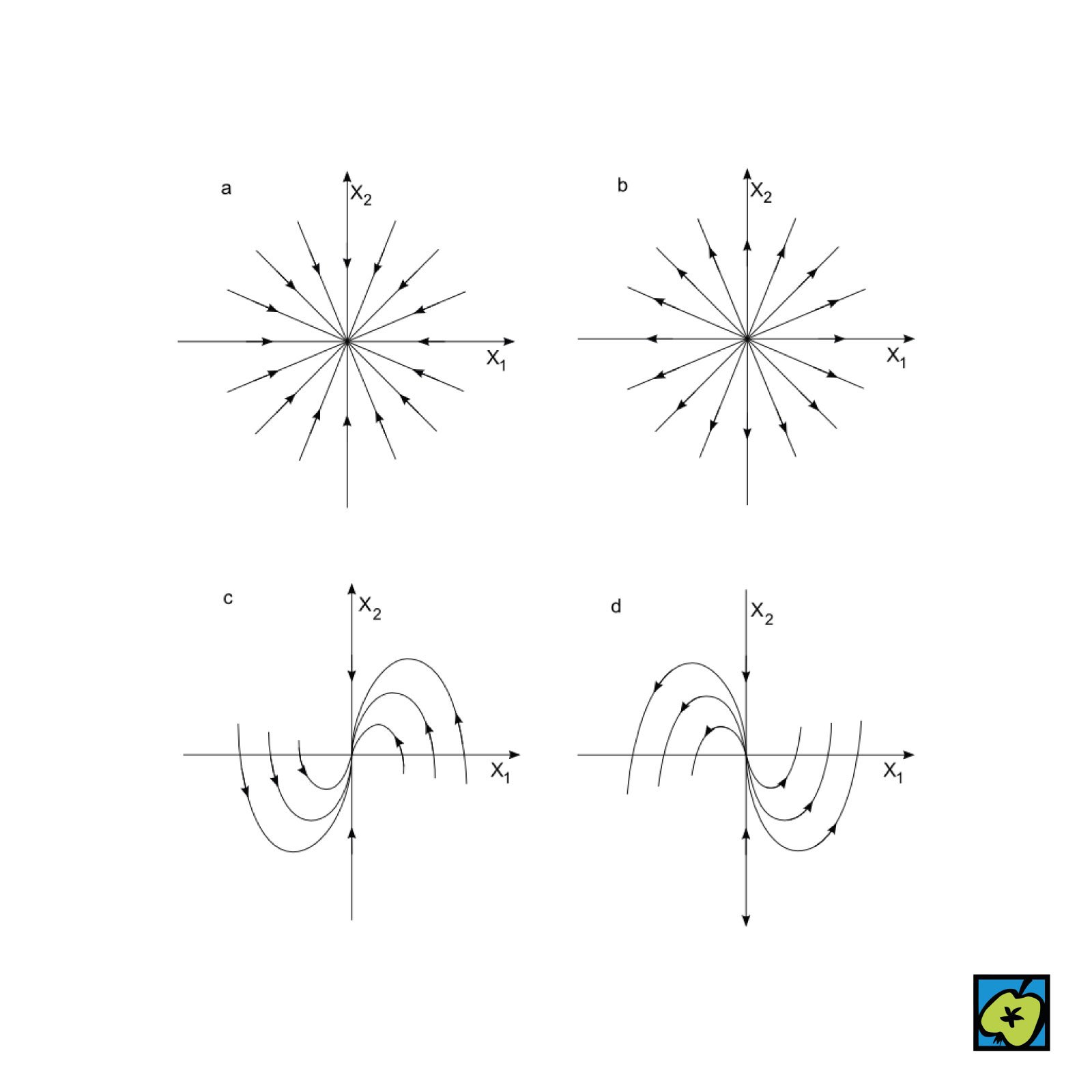
Dikritické uzly znázorněné ve fázovém prostoru: (a) stabilní uzel – všechny trajektorie směřují do bodu rovnováhy, (b) nestabilní uzel – všechny trajektorie vycházejí z bodu rovnováhy, (c) stabilní sedlový uzel – trajektorie se k bodu přibližují podél jedné osy a vzdalují podél druhé, (d) nestabilní sedlový uzel – opačný směr k (c), trajektorie směřují ven z bodu podél jedné osy a přibližují se po druhé – CoJeCo.cz (CC BY-SA 4.0)
